Assignment 10

Allison McNeece

For this assignment we will be looking at parametric equations.

A parametric curve in the plane is a pair of functions. x=f(t) and y=f(t) where f(t) is a function of time.

The two continuous functions define ordered pairs (x,y) and are called parametric equations of a curve.

The extent of the curve will depend on the range of t.

For example let's look at the following equations:

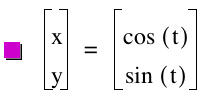
basic equations

Allowing t to range from 0 to π we get:

t ranging from 0 to pi

But if we allow t to rangle from 0 to 2π then we get:

t ranging from 0 to 2pi

What if we changed up these equations a bit?

Let's graph the following with different values for a and b and 0 < t < 2π

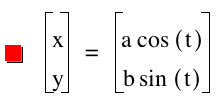
basic equations with a and b

with a=1 and b=1

with a=b

with a=2 and b=1

with a>b

with a=1 and b=2

with b>a

So this gives us the intuition that if a>b then our graph will be stretched out horizontally but if b>a then our graph will be stretched out vertically.

What if we manipulated the values of what we are taking the sine and cosine of?

Let's first place an n infront of the t in the cosine function and see what the graph looks like for different values of n:

(a=b=1 and 0<t<2π)

n is odd	n is even
n=1	n=2
n=3	n=4
n=5	n=6
n=7	n=8
n=9	n=10

So we find that there is a difference when n is even or odd. Well let's think about this, what do we know about cosine?

cos(π) = -1

cos(2π) = 1

Let's try this again but let's place an n infront of the t in the sine funtion:

with sin(nt)

(a=b=1 and 0<t<2π)

n is odd	n is even
n=1	n=2
n=3	n=4
n=5	n=6
n=7	n=8
n=9	n=10

We don't see the difference between even and odd values that we saw when looking at the cosine values.

What do we know about the sine function?

sin(π) = 0

sin(2π) = 0

return to my page